Section 3-1: The Definition of the Derivative. In the first section of the Limits chapter we saw that the computation of the slope of a tangent line, the instantaneous rate of change of a function, and the instantaneous velocity of an object at (x = a ) all required us to compute the following limit.
2.2 Definition Of Derivativeap Calculus Algebra
Click on the images to open a new tab and see them in full resolution.

2.2 Version 2 Answers
1. A rechargeable battery is plugged into a charger. The graph shows C(t), the percentage of full capacity that the battery reaches as a function of time t elapsed (in hours).
2. Let f(x) = x^3
3. Find the derivative of the function using the definition of the derivative. f(x) = 1x/2 – 1/10
4. Find the derivative of the function using the definition of the derivative.
F(x) = 7.5x^2 – x + 2.8
5. Find the derivative of the function using the definition of the derivative.
G(t) = 3/t^1/2
6. Find the derivative of the function using the definition of the derivative.
g(x) = sqrt(5 – x)
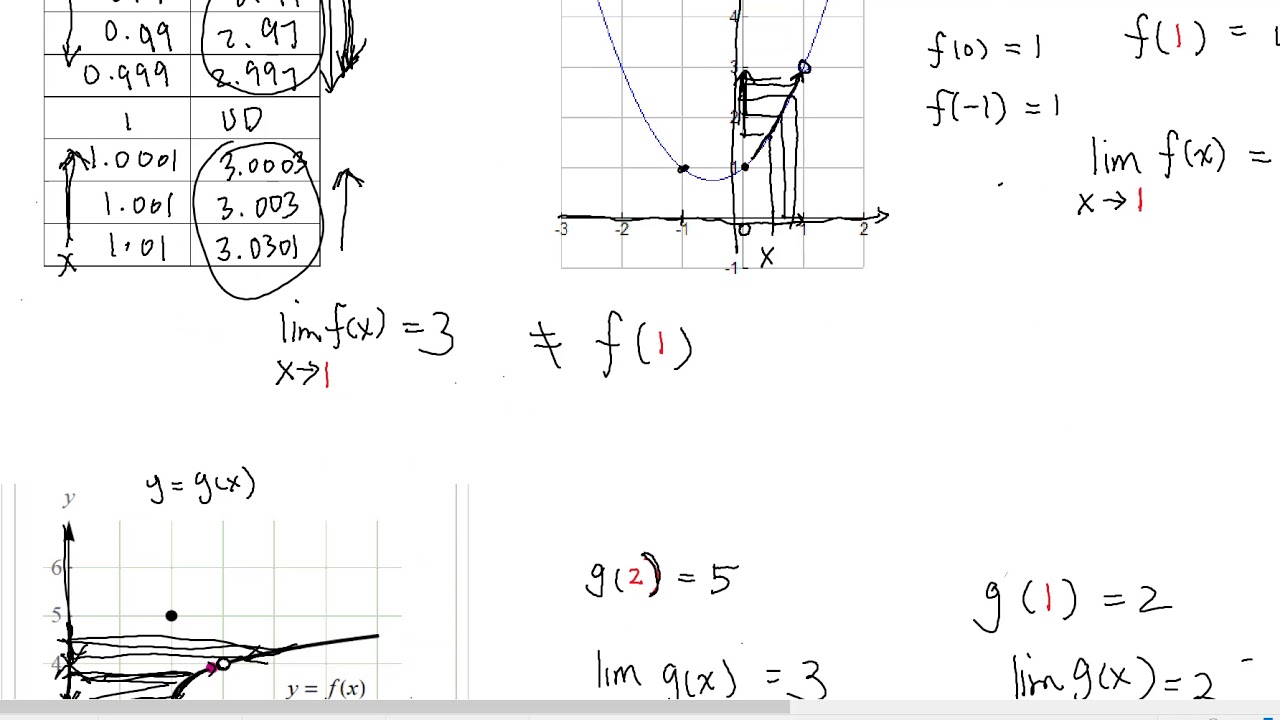
8.The graph of f is given. State the numbers at which f is not differentiable.
9. The graph of f is given. State the numbers at which f is not differentiable.
10. Use the definition of the derivative to find f’(x) and f’’(x).
f(x) = 4x^2 + 3x + 3
11. If f(x) = 2x^2 – x^3, find f’(x), f’’(x), f’’’(x), and f(4)(x).
12. If f(t) = t^1/3 and a cannot = 0, find f’(a).



2.2 Definition Of Derivativeap Calculus 14th Edition
- This chapter begins with the definition of the derivative. Two examples were in Chapter 1. When the distance is t2, the velocity is 2t. When f(t) = sin t we found v(t)= cos t. The velocity is now called the derivative off (t). As we move to a more formal definition and new examples, we use new symbols f' and dfldt for the.
- Chapter 2: Continuity & Limit Definition of Derivative AP Calculus Chapter 2 Review Sheet Section I: In the examples below, find the points of discontinuity of the function.
